See part 1 here.
In order to capture and decode more bits from the CD's surface, multiple images are needed. Below are 125 images forming a short arc (roughly following the CD's tracks) stitched with Hugin. (Other stitching tools include MIST and Ashlar, though MIST assumes a regular grid structure, so it's not suitable for this case.) The images are spaced by 60 microns, about 40% of the microscope objective's usable field of view. The positioning is not perfectly regular due to the limited precision of the stage.
Here's a zoomable image. The original image and the associated processing code are linked below.
The stitching does quite well, achieving about 0.02 pixels RMS of mismatch between corresponding features in overlapping images. (Hugin works with discrete features rather than image cross-correlation.) This is low enough to not induce significant jitter in the bit clock across the image boundaries.
Once we have the complete image, we can extract a single track for demodulation. As it happens, sampling along a circle is sufficiently accurate (the circle's center and radius were arrived at by trial and error). For larger images, an adaptive tracking scheme will be needed to stay on track, but that's a refinement for another day. This would be analogous to the track servo used in an actual CD player. (The other servo, for focus, is already handled by the microscope's image-acquisition script.)
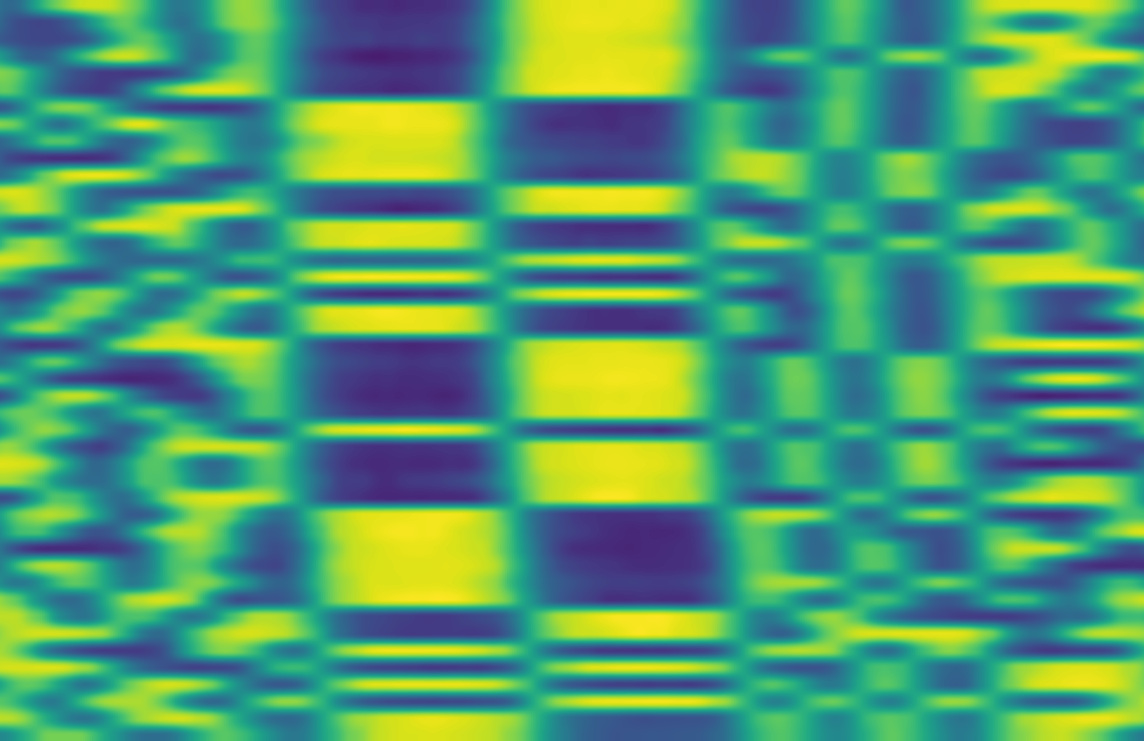
To acquire and maintain bit sync, the image below is useful. It consists of the track waveform sliced into individual 588-bit frames, then stacked row-by-row into a waterfall plot. The 24-bit frame-sync word, 111111111110000000000011 (or its inverse), is clearly apparent. Any clock error is visible as drift in the bit transitions. In this case, as a quick hack, I assembled a quadratic-spline approximation to the drift by picking a few points by hand in an image editor, then folding this correction into the resampling. Again, for a longer capture, adaptive clock recovery would be needed.
So finally we have about 40 frames, or 20000 channel bits, and this time we have sufficiently many bits to acquire frame sync and decode the inner RS code. (Unfortunately the outer RS code is separated from the inner by about 100 frames of interleaving, so we still can't quite get to final decoded audio samples.)
Below is the sequence of 40 frames in hexadecimal. The first column is the control/data byte (and indeed the pair of sync EFM symbols, S0 and S1, can be seen, although S0 is corrupted with a channel defect), and the other column groups are as follows: 12 bytes of audio, 4 bytes of outer RS parity, 12 more bytes of audio, and 4 bytes of inner RS parity. The red splotches show erasures from invalid EFM codewords.
After decoding the inner RS code (called the C1 code in the specification), the first few codewords are:
01 a7 fc 8b f9 f2 ff 9c 05 3f fe 4c b0 77 d7 e7 ff ae fb c6 03 62 03 db fb c8 04 ff 39 0d bc 53 fe a1 fe b9 fc c1 00 be 01 ea 03 d3 67 7d 2f 56 01 78 f6 67 01 91 03 41 fa 7c 09 93 98 c4 16 af ff 4b 00 a1 fd 45 00 db 00 03 05 c7 81 10 c2 4e 01 64 f8 f8 02 4f 02 f8 f9 ff 05 67 75 88 49 a8 00 b8 02 95 fe c3 fe 28 ff b6 02 f9 8e 9e 3c af 01 61 f9 4b ff 26 05 6c f6 4f 03 8f 09 d5 1a 64 fa f1 04 d2 fd f5 fc f2 fd 4f 04 47 07 a7 db 9f 02 48 f5 30 ff 0f 02 65 f4 3e 03 93 b2 09 f0 c7 fb 06 03 15 fd 43 ff c5 fe 59 05 af 57 85 8d b1 06 8a f6 bd fc 17 ff 23 f9 b1 04 46 77 9b 66 fc fc 6f 03 58 fb a8 02 cc ff ac 04 51 a3 8d b9 3a 06 e5 fa df fc ca 00 37 ff 2c fe 83 70 0d 1e f4 fc 27 04 c7 fc 7f fe c7 00 8e 06 85 4b 0a 8b 65 03 cd fc 04 fa 10 03 e4 00 76 fa 74 0d dc a6 b4 fb 55 00 fb fd 7a f8 94 ff d6 04 80 a7 10 b5 86 00 cb fe da f9 81 00 bc 04 4e fb 50 76 11 f9 c3 fa 52 fd cc fe 3b f9 34 01 e9 01 04 b6 5b eb 93 ff a2 02 a2 f7 4b 01 2b 02 1c f9 73 c6 43 37 a4
Code for all this can be found in my github repository. The repository's Makefile downloads the full stitched image and runs the processing pipeline. The full stitched image is also available here: cd-stitched.png (42k by 12k pixels, 36 MB).
The next step (sigh) is to go all the way around the disc. This will allow a long, continuous spiral to be extracted, and we can finally hear some audio.