It turns out to be an interesting exercise to extract the BeiDou B2b codes from GNSS recordings. If there were a pilot on B2b, there would have been plenty of SNR with even a short recording to see the pilot using a technique similar to that shown by Yudanov [1]. But, when assuming a pilot with period 100 ms, and then trying a great many other possible periods, there appeared to be nothing there.
As it turns out, there is no pilot. There are data signals on both B2bi and B2bq. One of them has what looks like a 2-second frame structure, but the data in the 2-second window changes periodically, so it is not a fixed pattern as the secondary code of a pilot would be.
So rather than coherently combining many samples of the pilot, we instead need to estimate the data symbols individually by differentially-coherently correlating a designated 1 ms interval with successive intervals. This entails a squaring loss. Even with signals of 45 to 47 dBHz during favorable passes, the QPSK data symbols are quite weak, and the chip decisions after noncoherently integrating for a few seconds are not error-free. But there is enough there to hard-limit the chip estimates, track the signal conventionally using this code-with-some-errors, and then use the track to refine the chip estimates to be truly error-free. (Perhaps there is some relationship to iterative decoding and belief propagation, and maybe a more sophisticated algorithm could deal optimally with even weaker signals.)
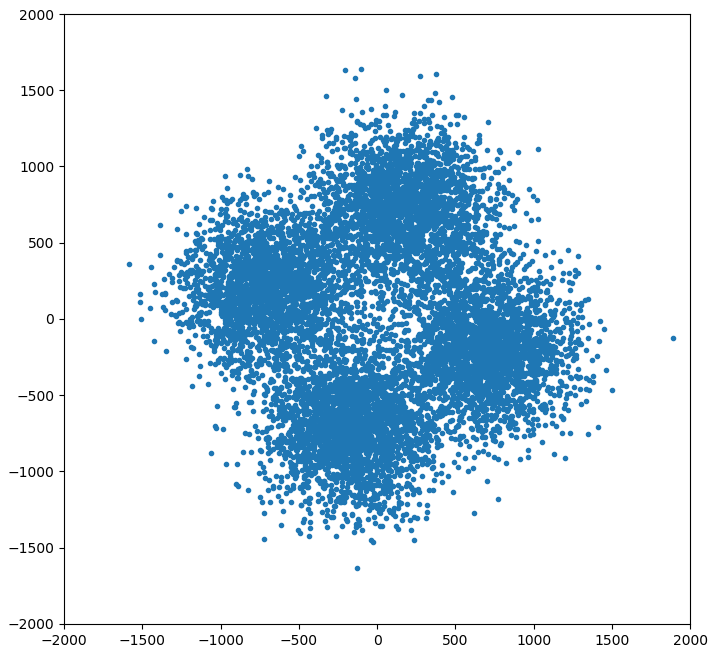
As an example, here is a plot of the QPSK B2b chips of BeiDou PRN 34, integrated for 4 seconds after wiping off the data modulation (using the unreliable estimates). The B2a signal is tracked (with its known code) to serve as a guide for code timing and to remove fluctuations of the local clock (a TCXO in my case). The carrier for B2b is then blindly applied as B2a + 30.69 MHz + a differential-doppler correction, which must be good to 0.1 Hz or so for the coherence to be maintained.
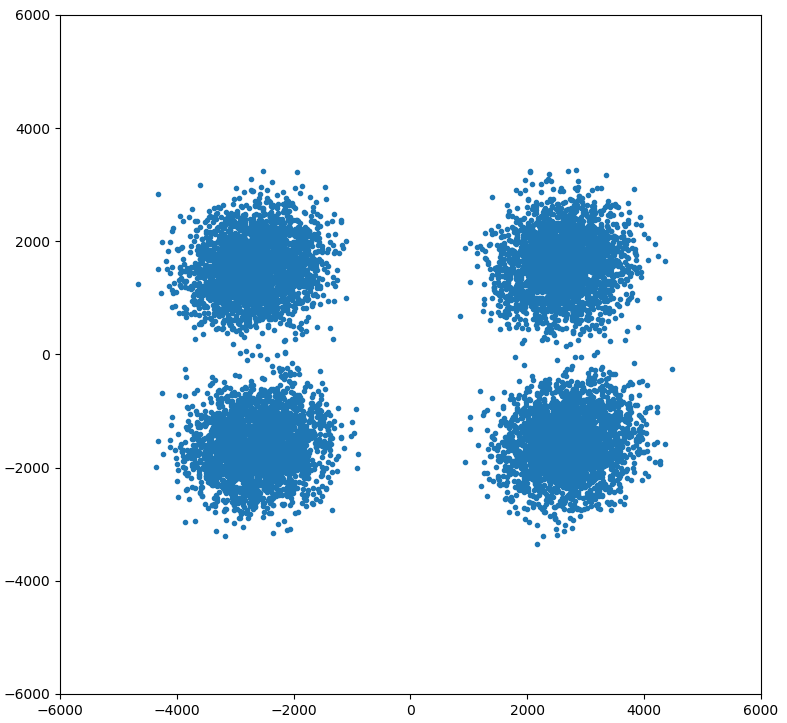
The real part of these chips (after rotating a bit), hard limited, is taken as the B2bi code, and the imaginary part the B2bq code. Re-tracking with those codes yields a very much improved estimate of the code chips. One of the two quadratures, call it B2bi_improved, is shown below; the other is very similar when tracked using the other code. (I'm a little puzzled by the discrete nature of the imaginary part of these chips; perhaps it represents part of the ACEBOC multiplex. But the code is just taken as the real part.)
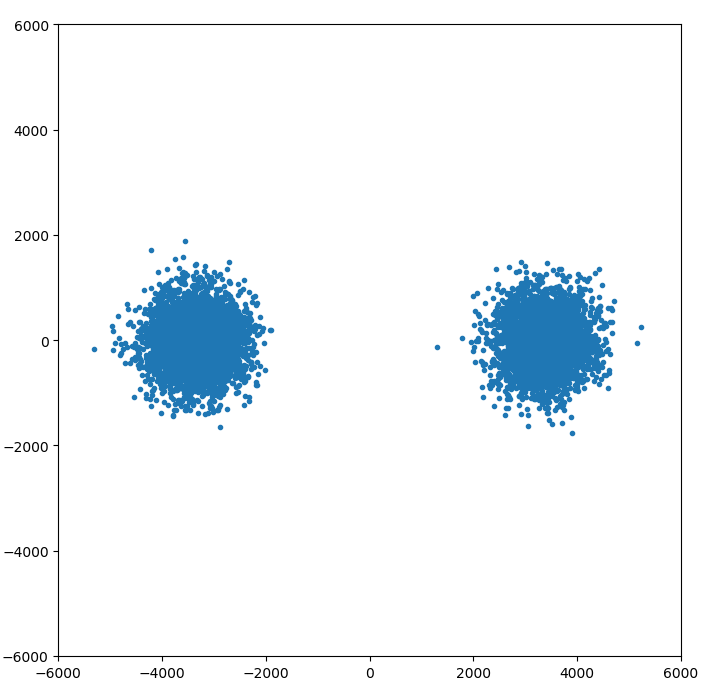
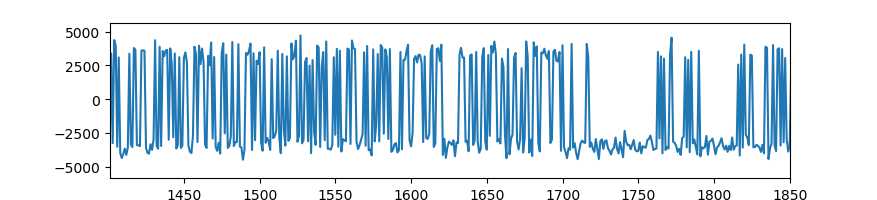
Tracking with this refined code yields the 1 ms data symbols shown below. Shown first are the complex values of the prompt correlator output (which are purely BPSK, showing that tracking is good), and second the real part over time, showing some of the structure of the data. (These are now the data symbols for B2bi over time, not the code chips.)
Codes for the current set of 18 MEO BeiDou-3 satellites are available here:
https://github.com/pmonta/GNSS-DSP-tools
Note that there is a 4-way ambiguity in each of these codes because of the (apparently equal-power) QPSK. But with the data format as yet unknown, this doesn't matter. Or, possibly, looking at B2a (for example by implementing B2ab tracking) could resolve the ambiguity.
It might be possible to reverse-engineer the B2b codes to some underlying Gold-code parameters, if they are in fact of similar provenance as B2a, but there seems to be no tangible benefit to doing that. I think I'll just leave them expressed as memory codes and wait for the ICD.
| [1] | Sergei Yudanov, A Case History Using the New Galileo E6-B/C Signal. https://www.gpsworld.com/signal-decoding-with-conventional-receiver-and-antenna-a-case-history-using-the-new-galileo-e6-bc-signal/ |